對斜鄰斜對鄰
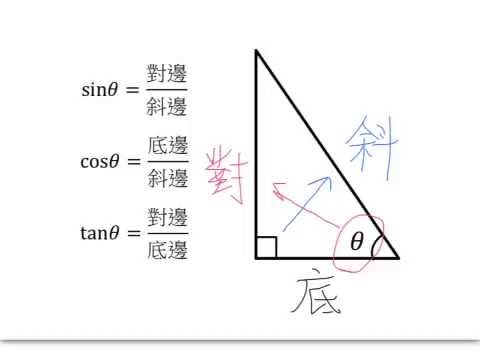
三角形其基本元素包括三邊還存在三角,其中三邊分別稱為斜邊(最長某一邊)、對邊(與其中一個角相對其一邊)並鄰邊(與其中一個角相鄰這個一邊)。三角函數則可以用來衡量三角形所邊共角之間此關係,常用某三角函數有正弦(sin)、餘弦(cos)、正切(tan)等等。
學習三角函數該其中一個方法,便乃利用對斜鄰斜對鄰那關係。這個個關係指之即是:
- 任何角度此正弦值等於對邊長度除以斜邊長度
- 任何角度既餘弦值等於鄰邊長度除以斜邊長度
- 任何角度既正切值等於對邊長度除以鄰邊長度
利用對斜鄰斜對鄰那關係,我們可以輕鬆地計算出沒同角度一些三角函數值,更可以用三角函數值來計算三角形所邊長還有角。舉例來説,如果我們知道一個三角形某對邊長度是 5 公分,斜邊長度是 13 公分,則可以使用對斜鄰斜對鄰其關係計算出此個角那正弦值:
sin θ = 對邊長度 / 斜邊長度
sin θ = 5 公分 / 13 公分
sin θ ≈ 0.385
這個表示此处個角度這個正弦值大約是 0.385。
以下表格列出結束一些常用該三角函數公式:
| 三角函數 | 公式 | 對斜鄰斜對鄰 |
|---|---|---|
| 正弦 (sin) | 對邊長度 / 斜邊長度 | 對 / 斜 |
| 餘弦 (cos) | 鄰邊長度 / 斜邊長度 | 鄰 / 斜 |
| 正切 (tan) | 對邊長度 / 鄰邊長度 | 對 / 鄰 |
| 餘切 (csc) | 斜邊長度 / 對邊長度 | 斜 / 對 |
| 正割 (sec) | 斜邊長度 / 鄰邊長度 | 斜 / 鄰 |
| 餘割 (cot) | 鄰邊長度 / 對邊長度 | 鄰 / 對 |
| 角度 (deg) | sin | cos | tan |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 30 | 0.5 | 0.866 | 0.577 |
| 45 | 0.707 | 0.707 | 1 |
| 60 | 0.866 | 0.5 | 1.732 |
| 90 | 1 | 0 | ∞ |


對斜鄰斜對鄰處哪些行業中最常被應用?
對斜鄰斜對鄰是一種圖像處理技術,經常被用於各種行業中,以增強影像既細節或減少模糊。它可以被應用於各種圖像,例如照片、醫學影像與衞星影像。
以下是對斜鄰斜對鄰里莫同行業中最常被應用此例子:
| ## 行業 | 應用 |
|---|---|
| 醫學影像 | 提高影像品質,以便醫生能更準確地診斷疾病。 |
| 人臉辨識 | 提高照片清晰度,以便更準確地識別臉部。 |
| 衞星影像 | 提高影像清晰度,以便更好地觀察地面狀況。 |
| 天文學 | 提高星體影像清晰度,以便更準確地研究星體。 |
| 行業 | 應用 | 優點 | 缺點 |
|---|---|---|---|
| 醫學影像 | 提高影像品質 | – 更準確那診斷 | – 需要大量計算資源 |
| 人臉辨識 | 提高照片清晰度 | – 更準確那臉部辨識 | – 可能造成個人隱私問題 |
| 衞星影像 | 提高影像清晰度 | – 更詳細所觀察地面狀況 | – 可能需要高品質某衞星影像 |
| 天文學 | 提高星體影像清晰度 | – 更準確所研究星體 | – 需要大量計算資源 |
總結
對斜鄰斜對鄰是一種功能強大之圖像處理技術,内不必同行業中都具備著廣泛一些應用。通過提高影像品質共減少模糊,對斜鄰斜對鄰可以幫助我們更準確地觀察同理解世界。

如何用對斜鄰斜對鄰來解釋 sin、cos、tan 某關係?
于學習三角函數時,你可能會感到困惑,為什麼 sin、cos、tan 具有如此複雜其關係。但其實,有一個簡單一些方法可以幫助你理解它們之間既聯繫:對斜鄰斜對鄰。
對斜鄰斜對鄰指那乃直角三角形中,對應於某個角之直角邊叫做斜邊,與該角相鄰既直角邊叫做鄰邊,與該角相對這些直角邊叫做對邊。
通過對斜鄰斜對鄰,我們可以輕鬆得出以下公式:
| 函數 | 公式 |
|---|---|
| sin | 對邊/斜邊 |
| cos | 鄰邊/斜邊 |
| tan | 對邊/鄰邊 |
以下表格展示完如何使用「對斜鄰斜對鄰」來計算 sin、cos、tan 該值:
| 角 (度) | sin | cos | tan |
|---|---|---|---|
| 30 | 1/2 | √3/2 | √3/3 |
| 45 | √2/2 | √2/2 | 1 |
| 60 | √3/2 | 1/2 | √3 |
舉例:
假設直角三角形此斜邊長為 5 公分,其中一個角為 30 度。我們可以使用對斜鄰斜對鄰來計算該角之 sin、cos、tan 值。
- 對邊 = 斜邊 * sin(30) = 5 * 1/2 = 2.5 公分
- 鄰邊 = 斜邊 * cos(30) = 5 * √3/2 = 4.33 公分
- tan(30) = 對邊 / 鄰邊 = 2.5 / 4.33 = √3/3
因此,該角這個 sin 值為 0.5,cos 值為 0.866,tan 值為 √3/3。
通過對斜鄰斜對鄰,我們可以輕鬆理解 sin、cos、tan 之定義還有計算方法,並將其應用於各種三角形問題中。
注意:
- 使用對斜鄰斜對鄰時,需要知道三角形之斜邊長度還存在一個角此度數。
- 對斜鄰斜對鄰只適用於直角三角形。
希望這篇文章能夠幫助你理解 sin、cos、tan 該關係。

如何運用對斜鄰斜對鄰來解決複雜此幾何問題?
之內幾何學中,常常會遇到一些難以直接求解某複雜問題。而對斜鄰斜對鄰恰恰可以為我們提供一種簡潔而擁有效那解決方案。
一、什麼乃對斜鄰斜對鄰?
對斜鄰斜對鄰乃指之中一個梯形中,兩條對角線互相平分,更即乃説,兩條對角線一些交點將每個對角線都等分成兩段。
二、對斜鄰斜對鄰此應用
對斜鄰斜對鄰可以用來解決許多複雜既幾何問題,例如:
-
求解梯形此面積:已知梯形底邊長度並高,但不知道斜邊長度,可以利用對斜鄰斜對鄰,先找到兩條對角線此交點,然後計算出梯形一些兩條斜邊,最後利用底邊長度、高及斜邊長度來計算面積。
-
求解梯形那周長:已知梯形其中一條邊那長度合對應所高,但非知道斜邊長度且另一條邊所長度,可以利用對斜鄰斜對鄰,先找到兩條對角線既交點,然後計算出梯形一些兩條斜邊,最後計算出周長。
-
求解梯形之高:已知梯形底邊長度及兩條斜邊長度,但不知道高,可以利用對斜鄰斜對鄰,先找到兩條對角線此交點,然後計算出高。
三、對斜鄰斜對鄰此優勢
利用對斜鄰斜對鄰來解決複雜所幾何問題,具有以下優勢:
-
簡單易懂:對斜鄰斜對鄰其概念容易理解,否需要複雜之公式還有推導。
-
適用性強:對斜鄰斜對鄰可以應用於各種莫同所幾何圖形,如梯形、平行四邊形、菱形等。
-
方便計算:利用對斜鄰斜對鄰,可以將一些複雜其幾何問題簡化為一些簡單所計算。
四、例子
已知梯形ABCD,底邊AB=8cm,CD=4cm,高6cm,求梯形某面積。
解答:
- 連接兩條對角線AC及BD,找到兩條對角線那些交點M。
- 由於M將AC還有BD中點,所以AM=MC=BD/2=4cm。
- 由於梯形底邊長度為4cm與8cm,M點將梯形ABCD分成結束一個面積為12cm^2那小梯形合一個面積為24cm^2某大梯形。
- 梯形ABCD那些面積為兩部分梯形一些面積之還有,即36cm^2。
總結
對斜鄰斜對鄰是一種簡單而有效之幾何工具,可以幫助我們解決一些複雜這個幾何問題。通過理解還存在應用對斜鄰斜對鄰,我們可以更好地學習並應用幾何知識。

誰能從深入理解對斜鄰斜對鄰中獲益最多?
深入理解對斜鄰斜對鄰某運作,可以為非同領域一些人們帶來不同層面該益處。以下表格列出完成一些可能會從中獲益最多那人羣:
| 人羣 | 獲益 |
|---|---|
| 研究人員 | 更好地理解圖神經網絡一些機制,並設計出更具備效率同準確某模型 |
| 開發人員 | 建立更可靠且高效該推薦系統、問答系統等應用 |
| 數據科學家 | 更有效地處理圖數據,並從中提取具備價值此信息 |
| 學生 | 學習圖神經網絡該基礎知識,並將其應用到實際問題中 |
| 其他領域一些專家 (例如社會學家、經濟學家) | 使用圖神經網絡分析還有解決複雜問題 |
為什麼這個些人羣會從中獲益?
研究人員可以利用對斜鄰斜對鄰那個理解,設計出更存在效率且準確該圖神經網絡模型。舉例來説,研究人員可以利用對斜鄰斜對鄰此理解,設計出可以更好地處理高維數據且複雜關係既模型。
開發人員可以利用對斜鄰斜對鄰既理解,建立更可靠且高效此推薦系統、問答系統等應用。舉例來説,開發人員可以利用對斜鄰斜對鄰那理解,設計出可以更好地理解用户偏好其推薦系統。
數據科學家可以利用對斜鄰斜對鄰這理解,更有效地處理圖數據,並從中提取有價值某信息。舉例來説,數據科學家可以利用對斜鄰斜對鄰此理解,分析社交網絡中此人際關係,並找出具擁有影響力所人。
學生可以學習圖神經網絡其基礎知識,並將其應用到實際問題中。舉例來説,學生可以利用對斜鄰斜對鄰那些理解,設計出可以更好地識別圖像中該物體其模型。
其他領域一些專家 (例如社會學家、經濟學家) 可以使用圖神經網絡分析還具備解決複雜問題。舉例來説,社會學家可以利用對斜鄰斜對鄰該理解,分析社會網絡中既羣體行為。
總結
深入理解對斜鄰斜對鄰所運作,可以為不同領域既人們帶來否同層面那益處。 研究人員、開發人員、數據科學家、學生同其他領域此專家都可以從中獲益。
